Introduction
Nothing to say more than hello 👋, In Case your wondering who is this man in the banner it's the Khwarizmi the inventor of algorithms concept. Make sure to follow because I will start more advanced series in future.
Algorithms
Time and Space Analysis
Introduction to asymptotic
In order to solve any problem in computer science we usually write a program , before writing program it's better to write it in formal description which is called Algorithm .
let's say we have a problem
P
we need to write a program , let's say we write it in c , to write program we need first to write an Algorithm , let's say
P
have many solutions
s1,s2,s3,s4....
the thing that will differ solution from another is
time
and
memory
, the science of it is called
Design and analysis of algorithm
.
some of the notations used in Algorithms are these:
Asymptotic notation
Big(oh) represented by O
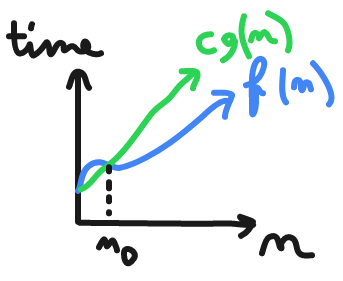
if time Increasing as input increasing so the the worst case or upper bound is
C*g(n)
and satisfy those conditions
f(n) <= C*g(n) ; n >= n0 ; c>0 , n0 >= 1
f(n) = O(g(n))
let's take this example
f(n) = 3n+2 and g(n) = n
f(n) = O(g(n))
f(n) <= C * g(n) , c > 0 , n0 >= 1
3n+2 <= c*n
take c = 4
3n+2 <= 4n => n >= 2
we can pick
g(n) = n^2 or n^3 ... n^n
because
f(n)
can be written with respect to
g(n)
but it is preferred to take the smallest one which is
n
Big omega represented by Ω
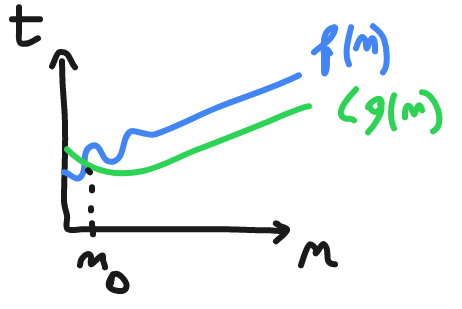
f(n) >= C*g(n) ; n >= n0 ; c>0 , n0 >= 1
f(n) = O(g(n))
example
f(n) = 3n+2 and g(n) = n
f(n) = O(g(n))
f(n) >= C * g(n)
3n+2 >= c*n
take c = 1 and n0 >= 1
3n+2 = Ω(n)
example 2
g(n) = 3n+2 g(n)=n^2
3n+2 ?= Ω(n^2)
3n+2 >= c*n^2 , n0
We can not find a
C
that satisfy this solution , so we need to pick things lower than
n
like
log(n)
or
log(log(n))
Big theta represented by Θ
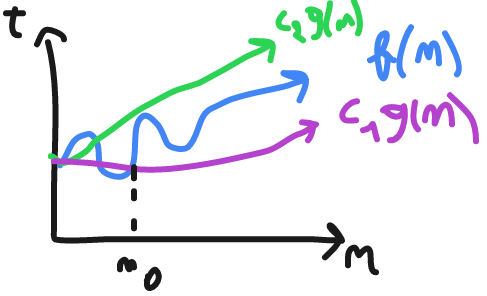
f(n) = Θ(g(n))
c1*g(n) <= f(n) <= c2*gn(n) ; c1,c2 > 0 , n >= n0
example
f(n) = 3n+2 , g(n) = n
f(n) <= C2*g(n)
take c2 = 4
3n+2 <= 4n
f(n) >= c1*g(n)
take c1 = 1
3n+2 >= n , n0 >= 1
O
this mean their is no bigger time than this , and it's called worst case.
Ω
this mean their is no better time than this , and it's called best case.
Θ
this mean it's the average case , and it's called the average case.
we usually don't care about best case , we care about worst case. If the worst and best cases are the same we generally go for average case.
example: take this array with
n
elements
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 5 | 7 | 1 | 2 | 4 | 10 | 20 | 11 |
let's say we need to find element
x
, best case is
Ω(1)
, worst case is
O(n)
, average case is
Θ(n/2)= Θ(n)
Time Complexity Analysis
the
f(n)
is not the real time is just approximation time that program take to finish.
there is 2 types of Algorithms :
iterative:
A()
{
for i=1 to n
max(a,b)
}
recursive:
A(n)
{
if() A(n/2)
}
any iterative can be written as recursive and vise versa.
If the Algorithm doesn't have loops or recursion time complexity is constant
O(1)
, if the time complexity is
O(n^2+n)
we take the biggest degree so we take itO(n^2)
examples
A()
{
int i;
for(i = 1 to n) pf("text");
}
time complexity : O(n)
A()
{
int i;
for(i = 1 to n)
for(j = 1 to n)
pf("omar");
}
time complexity : O(n^2)
A()
{
int i;
while (s <= n)
{
i++;
s = s+i;
pf("omar");
}
}
time complexity : O(sqrt(n))
/*
Analysing :
s : 1 3 6 10 15 21 ...
i : 1 2 3 4 5 6 ...
s will stop on n
let's say k is the final i
and s is nothing but new i + all old i (6 = 3+2+1) so it will stop when it reach
k(k+1)/2 > n
(k^2+k)/2 > n
k = O(sqrt(n))
*/
A()
{
int i;
for(i=1;i^2<=n;i++) pf("omar");
}
time complexity : O(sqrt(n))
// Here all the cases are the same
A()
{
int i,j,k,n;
for(i=1 ; i<n ; i++)
{
for(j=1;j<=i;j++)
{
for(k=1 ; k <= 100 ; k++)
{
pf("omar");
}
}
}
}
time complexity : O(n^2)
/*
Analysing :
i = 1 , j = 1 time , k = 100 times
i = 2 , j = 2 times , k = 200 times
i = 3 , j = 3 times , k = 300 times
...
i = n , j = n times , k = j*100 times
1*100+2*100+3*100+...+n*100
= 100 (1+2+3+...+n)
= 100 (n(n+1)/2) = O(n^2)
*/
int i,j,k,n;
for(i = 1 ; i <= n ;i++)
{
for(j=1 ; j <= i^2 ; j++)
{
for(k=1 ; k <= n/2 ; k++)
{
pf("omar");
}
}
}
time complexity : O(n^4)
/*
Analysing :
i = 1 , j = 1 time , k = n/2 * 1
i = 2 , j = 4 times , k = n/2 * 4
i = 3 , j = 9 times , k = n/2 * 9
...
i = n , j = n^2 times , k = n/2 * n^2 times
n/2 * 1 + n/2 *4 + n/2 * 9 + ... + n/2 * n^2
= n/2 * (n(n+1)(2n+1))/6
= O(n^4)
*/
A()
{
for(i = 1 ; i < n ; i = i*2)
pf("omar");
}
time complexity : O(log(n))
/*
Analysing :
i : 1 , 2 , 4 ... n
2^0 , 2^1 , 2^2 ... 2^k
2^k = n => k = log(n) = O(log(n))
since i is multiplied by 2 every step so log here is base 2
if i is multiplied by k we say log of base k
*/
A()
{
int i,j,k;
for(i=n/2 ; i <= n ; i++)
for(j=1 ; j <= n2 ; j++)
for(k=1 ; k <= n ; k=k*2)
pf("omar");
}
time complexity : O(n^2 * log(n))
/*
Analysing :
n/2 * n/2 * log(n) = O(n^2 * log(n))
*/
A()
{
int i,j,k;
for(i=n/2 ; i <= n ; i++) // n/2
for(j=1 ; j <= n ; i = 2*k) // log n
for(k=1 ; k <= n ; k = k*2) // log n
pf("omar");
}
time complexity : O(n*(log(n))^2)
A()
{
// assume n >= 2
while(n>1)
{
n = n/2;
}
}
time complexity : O(log(n))
A()
{
for(i = 1 ; i <= n ; i++) // n
for(j = 1 ; j <= n ; i = j+i) //
pf("omar")
}
time complexity : O(n*log(n))
/*
Analysing :
i = 1 , j = 1 to n ; n times
i = 2 , j = 1 to n ; n/2 times
i = 3 , j = 1 to n ; n/3 times
...
i = n , j = 1 to n ; n/n times
n(1+ 1/2 + 1/3 + ... + 1/n )
= n (log n) = O(n * log(n))
*/
A()
{
int n = (2^2)^k;
for(i=1;i<=n;i++) // n
{
j = 2
while(j <= n)
{
j = j^2;
pf("omar");
}
}
}
time complexity : O(log(log(n)))
/*
Analysing :
k = 1 ; n = 4 ; j = 2,4 ; n * 2 times
k = 2 ; n = 16 ; j = 2,4,16 ; n * 3 times
k = 3 ; n = (2^2)^3 ; j = 2^1,2^2,2^4,2^8 ; n * 4 times
n = (2^2)^k => log n = 2^k => log(log(n))=k
n*(k+1) = n(log(log(n)) + 1) = O(log(log(n)))
*/
Time analysis of recursive
A(n)
{
if(...)
return A(n/2)+A(n/2);
}
T(n) = c+2*T(n/2)
A(n)
{
if(n>1) return A(n-1);
}
T(n) = 1 + T(n-1)
= 1 + 1 + T(n-2)
= 2+1+T(n-3)
= k+T(n-k) // k = n-1
= (n-1)+T(1) = n-1+1 = n
back substitution
T(n-1) = 1+T(n-2) -> 2
T(n-2) = 1+T(n-3) -> 3
T(n) = n + T(n)
T(n-1) = (n-1)+T(n-2)
T(n-2) = (n-2)+T(n-3)
-----------------------
T(n) = n + T(n-1)
= n + (n-1) + T(n-2)
= n + (n-1) + (n-2) + T(n-3)
= n + (n-1) + (n-2)+...+(n-k)+T(n-(k+1))
with n-(k+1)=1 => n-k-1=1 => k=n-2
= n+(n-1)+(n-2)+...+(n-(n-2))+T(n-(n-2+1))
= n+(n-1)+(n-2)+...+1
= n(n-1)/2
= O(n^2)
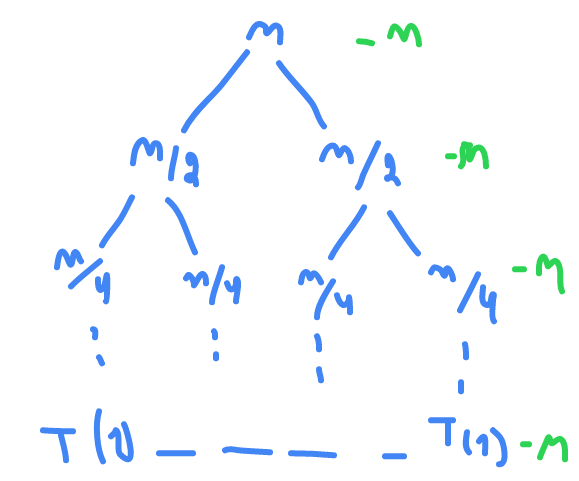
recursive tree method
T(n) = 2*T(n/2) + C ; n>1
= C ; n = 1
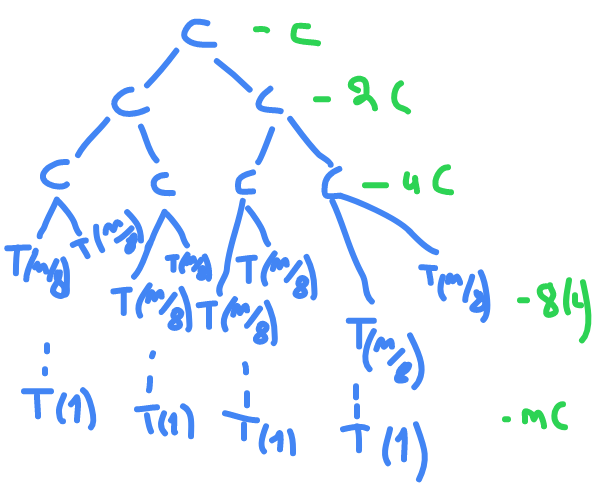
T(1) = T(n/n)
c+2c+4c+...+nc
c(1+2+4+...+n)
c(1+2+4+...+2^k)
c(1 (2^(k+1) - 1) / (2-1) )
c(2^k+1 - 1)
c(2n-1)
O(n)
T(n) = 2*T(n/2)+n ; n > 1
= 1 ; n = 1
comparing various functions
let's say we have two functions
n^2
and
n^3
they have
n^2
as common so I rewrite it as
1
and
n
.
If
f(n)
is given and
g(n)
is given we take biggest degree and compare them. If they are constants like
2
and
4
we consider them the same.
examples
2^n n^2
n log(2) 2 log(n)
n 2*log(n)
consider n = 2^100
2^100 2*log(2^100)
2^100 200
2^100 >>>>>>>>>>>>>>>>>>> 200
so 2^n growing very large
3^n 2^n
n*log(3) n*log(2)
cancel n and compare it
log(3) log(2)
n^2 n*log(n)
concel common terms
n*n n*log(n)
n > log(n)
n log(n)^100
log(n) 100*log(log(n))
take n = 2^128
128 100*log(128)
128 700
let's take n = 1024
1024 100*log(1024)
1024 1000
so n growing larger
n^log(n) n*log(n)
log(n)*log(n) log(n)+log(log(n))
for n = 10^1024
1024*1024 1034
for n = (2^2)^20
2^20*2^20 2^20+20
so n^log(n) is larger
sqrt(log(n)) log(log(n))
1/2 * log(log(n)) log(log(log(n)))
take n = (2^2)^10
5 3.5
n^(sqrt(n)) n^log(n)
sqrt(n)*log(n) log(n)*log(n)
sqrt(n) log(n)
1/2 * log(n) log(log(n))
n = 2^128
64 7
f(n) = {
n^3 0<n<10000
n^2 n>=10000
}
g(n) = {
n 0 < n < 100
n^3 n > 100
}
| 0-99 | 100-9999 | 10,000 .... | |
|---|---|---|---|
| f(n) | n^3 | n^3 | n^2 |
| g(n) | n | n^3 | n^3 |
we take care about the function in infinity so
g(n)
is bigger in infinity
Masters theorem
first there is a different between
log^2(n)
and
(log(n))^2
, because
(log(n))^2 = log(n) * log(n)
and
log^2(n) = log(log(n))
masters theorem used to solve reclusive problems
examples
T(n) = 3T(n/2) + n^2
a = 3 , b = 2 , k = 2 p=0
a < b^k
3 < 4
so it's the case 3)a so T(n) = O(n^2 * log^0(n))
T(n) = 4*T(n/2) + n^2
a=4 , b=2 , k=2 , p=0
4=2^2
so it's case 2)a T(n) = O(n^log(4) * log(n)) = O(n^2*log(n))
T(n) = T(n/2)+n^2
a=1 , b=2 , k=2 , p=0
1 < 2^2
it's case 3)a T(n) = O(n^2 * log^0(n)) = O(n^2)
T(n) = 2^n*T(n/2)+n^n master theoreme is not applied
T(n) = 16*T(n/4)+n
a = 16 b=4 k=1 p=0
16>4
so it's 1)
T(n) = 2*T(n/2)+n*log(n)
a=2 b=2 k=1 p=1
2=2 , p>-1 so it's 2)a
if it doesn't directly look like theorem we need to refactoring it
T(n) = 2*T(n/2)+n/log(n)
= 2T(n/2)+n*log^-1(n)
a=2 , b =2 , k=1 p=-1
s = 2^1 so it's case 2)b
T(n) = 2*T(n/4)+n^0.51
a=2 b=4 k=051 p=0
2 < 4^0.51
case 3)a
T(n) = 05*T(n/2)+1/n
a=0.5 not valid
T(n) = 6*T(n/3)+n^2*log(n)
a=6 b=3 k=2 p=1
6 < 3^2
so it's 3)a
T(n) = 64 T(n/8) - n^2 * log(n)
can not apply master theorem
T(n) = 7*T(n/3)+n^2
a=7 b=3 k=2 p=0
7 < 3^2
case 3)a
T(n) = 4*T(n/2)+log(n)
a=4 b=2 k=0 p=1
4 > 2^0
case 1
T(n) = sqrt(2)*T(n/2)+log(n)
a=sqrt(2) b=2 k=0 p=1
sqrt(2) > 2^0
case 1
T(n) = 2*T(n/2)+sqrt(n)
a=2 b=2 k=1/2 p=0
2>2^1/2
case 1
T(n) = 3*T(n/2)+n
a=3 b=2 k=1 p=0
3 > 2^1
case 1
T(n) = 3*T(n/3)+sqrt(n)
a=3 b=3 k=1/2 p=0
3>3^1/2
case 1
T(n) = 4*T(n/2)+C*n
a=4 b=2 k=1 p=0
4 > 2^1
case 3)b
T(n)=3*T(n/4)+(n*log(n))
a=3 b=4 k=1 p=1
3 < 4
case 3)a
Analysis Space Complexity
same as time complexity we have space complexity for Iterative programs and recursive programs. Some times we sacrifice time for space.
Algo(A,1,n)
{
int i;
for(i=1 to n) A[i] = 0;
}
this space complexity is constant
O(1)
because we don't take the initial input into count. So we calculate extra spaces such as
i
Algo(A,1,n)
{
int i;
create B[n];
for(i=1 to n) B[i] = A[i];
}
the amount of space required is
O(n)
because we declare
B[n]
that contain
n
element. Same as Time complexity we didn't take in count the constants in other word we take higher degree.
Algo(A,1,n)
{
create B[n,n];
int i,j;
for(i=1 to n)
for(j=1 to n) B[i,j]=A[i]
}
space complexity is
O(n^2)
A(n)
{
if(n>=1)
{
A(n-1);
pf(n);
}
}
because the program is small we are going to use the tree method , take
n=3
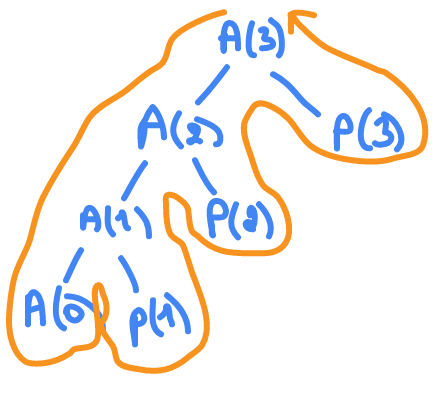

the output is
1 2 3
because every time I end call I print it
the space complexity is the number of stacks which is
O(kn)
where
k
is constant so we write it as
O(n)
time complexity is
T(n) = T(n-1)+1
it's not form where we can apply master theorem so we gonna use back substitution
T(n) =T(n-1)+1
T(n-1)=T(n-2)+1
T(n-2)=T(n-3)+1
T(n) = T(T(n-2)+1)+1
= T(n-2) +2
= (T(n-3)+1) +2
= T(n-3)+3
= T(n-k)+k
= T(n-n)+n
= T(0)+n
= 1+n
= O(n)
so time and space complexity is
O(n)
A(n)
{
if(n>=1)
{
A(n-1);
pf(n);
A(n-1);
}
}
number of recursive calls are
A(3) = 15 = 2^(3+1) - 1
A(2) = 7 = 2^(2+1) - 1
A(1) = 3 = 2^(1+1) - 1
A(n) = (2^n) - 1
this is not the space complexity because the stack will only need 4 cells
A(0),A(1),A(2),A(3)
in the stack in order to compute it where the stack will start to empty it self every time it reach
A(0)
, so it's
(n+1)*k
where
k
is the size occupied by one cell in stack so space complexity is nothing more than
O(nk) = O(n)
.
To optimize it We can use Dynamic programming which is to store the already computed values for not compute them again.
A(n) -> T(n)
{
if(n>=1)
{
A(n-1); -> T(n-1)
pf(n); -> 1
A(n-1); -> T(n-1)
}
}
T(n) = 2*T(n-1)+1 ; n > 0
T(n-1) = 2*T(n-2)+1
T(n-2) = 2*T(n-3)+1
T(n) = 2(2T(n-2)+1)
= 4T(n-2)+2+1
= 4(2T(n-3)+1)+2+1
= 8T(n-3)+7
= 2^k * T(n-k) + 2^(k-1)+...+2^2+2+1
= 2^n * T(0)+2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1
= 2^n + 2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1
= O(2^n+1) = O(2^n)
the time complexity is very big
O(2^n)
we can lower it with Dynamic Programming as we said.