Graphs

graph theory is in general an algebra class to study relationships between things , in computer science the most common use is the networking.
Representation of Graphs
first representation is
adjacency matrix
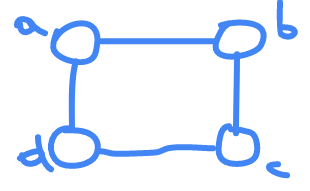
ever case represent the link between point and another as example
a
doesn't have a relation with it self , while
a
have relation with
b
and
a
doesn't have direct relation with
c
| a | b | c | d | |
|---|---|---|---|---|
| a | 0 | 1 | 0 | 1 |
| b | 1 | 0 | 1 | 0 |
| c | 0 | 1 | 0 | 1 |
| d | 1 | 0 | 1 | 0 |
another popular representation is
linked list
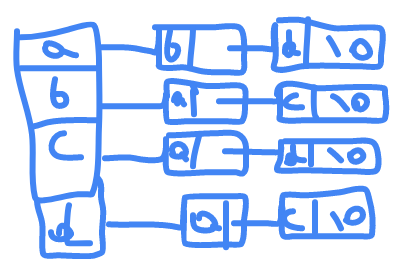
every node have pointer to nodes that connects to.
a dense graph it's a graph that have lot of connections between it nodes.
if the dense is
E=O(v^2)
where
E
is the number of edges and
v
is the number of vertexes , and it mean that graph had lot of connection between them self , in other words matrix is almost all 1 .
let's say we need a similar network for any social platform , the linked list make more sense because we are not going to connect with all in the network just with few friends.
and the order of linked list is
O(V+2E)
which is
<O(v^2)
BFS and DFS
Visited mean that I visit or print it.
Explored mean that I explore all the connections that she made (Neighbors).
| visited | explored | meaning |
|---|---|---|
| 0 | 0 | not visited and not explored |
| 1 | 0 | visited but not explored |
| 1 | 1 | visited and explored |
you can use array for check visited nodes , for explorer there algorithms that use
Queue
or
Stack
, the one that use
Queue
is called
BFS (Breadth First Search)
and the one that use the
stack
called
DFS (Depth First Search)
BFS
will traverse the tree like this
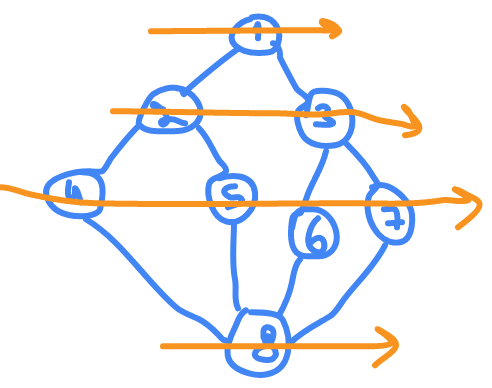
DFS
will traverse the tree like this
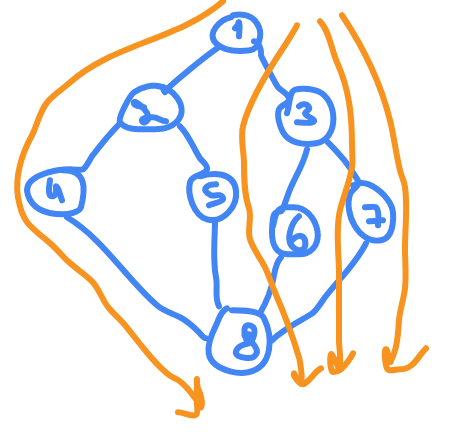
BFS algorithm
// the graph G and array visited[] are global
// visited[] is initialized to 0
BFS(v)
{
u = v;
visited[u] = 1;
repeat
{
for all vertices w adj to u do
{
if(visited == 0)
{
add w to q;
visited[w] = 1;
}
}
if q is empty then return;
delete the next element u from q;
}
}
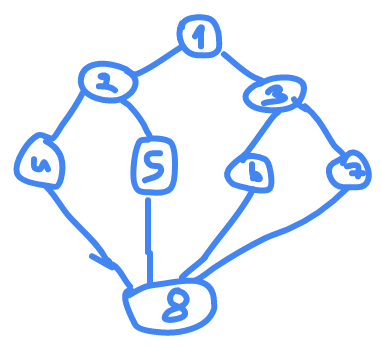
graph
G
visited
array is initialized to
0
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
queue
q
first iteration
u=1
and vertices
w
adj to
u
are
w={2,3}
, so visited and queue will be
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 |
after adding it to the queue
2
will be marked as visited
visited
array is initialized to
0
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
now we finish from
2
we need to go to
3
because we have a
for
loop here to go to all adjacent of
1
which they are
{2,3}
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 |
now we finish the
for
loop
q
is not empty so we are going to delete the next element from
q
which is
2
, now our
u
become
2
and neighbors of
2
are
w={1,4,5}
since
1
is visited we are not going to visit it again and we do same logic as before until we reach an empty
q
which mean all are visited and explored.
BFS analysis on linkedlist
the queue implementation will take space complexity of
O(v)
the linkedlist will take
O(v+E)
BFS analysis on adjacency matrix implementation
if we have
8
vertexes it mean we need a matrix of
8x8
size , the array and Queue implementation of it each will have space complexity of
O(v)
where v is number of vertexes , and the time complexity is
T(v^2)
Breadth First Traversal using BFS
in order to know if the graph is connected , it mean all the nodes are in same graph
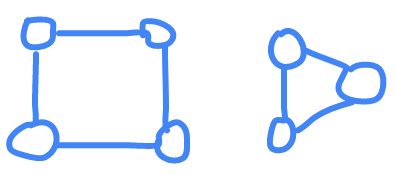
those can be separated into 2 graphs
U
and
G
there at least one node that doesn't have intersection from
U
with
V
to traverse those two sub graphs
BFT(G,n)
{
// this loop to fill the array with not visited yet
for i=1 to n do
visited[i] = 0
// this will visit every node that is not visited yet
for i=1 to n do
if(visited[i]==0) then BFS(i) //BFS not BFT !!!!!
}
let each case represent a Node
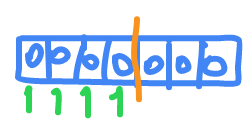
the first
4
boxes are the
U
graph with
4
nodes , he will start from 1 and mark from
1->4
as visited , then he will break.
after this it will start with
V
and do same thing.
time complexity is
O(E+V)
and space complexity
O(V)
DFS Algorithm
DFS(v)
{
visited[v] = 1;
for each vertex w adj to v do
{
if(visited[w] == 0) then
DFS(w);
}
}
in
DFS
we start with a point and explore it , if the next node in it not explored we leave the previous node and explore the new node.
initializing the visited array is done in the program that called the function , and we take it in count when we calculate the time complexity.

| V=1 | V=2 | V=4 | V=8 | V=5 | V=6 | V=3 | V=7 |
|---|---|---|---|---|---|---|---|
| w={2,3} | w={1,4,5} | w={2,8} | w={4,5,6,7} | w={2,8} | w={3,8} | w={1,7} | w={3,8} |
| 2 not visited | 4 not visited | 8 not visited | 5 not visisted | all w visited we go back to v=8 , 6 not visited | 8 not visisted | all w visited we go back to v=8 , 7 not visited | all w visited , and all V are visited |
as we see every time we have an unvisited node we fully explore it neighbors. if all the neighbors are visited we go back into old neighbors.
Analysis of DFS and DFT
space complexity of
DFS
is
O(V)
, the worst case if the graph is chain , because all the nodes will be on the stack in same time. So space complexity for
DFS
and
BFS
is
O(v)
, time complexity is
O(E)+O(V)
for the linked list representation where
O(V)
is time to initialize the visited array and
O(V^2)
for matrix representation , same as
BFS
.
DFT
will be the same as
BFT
instead of calling
BFS
we call
DFS
.