Binary trees are those who have max 2 childs , there are 3 types of binary tree traversal

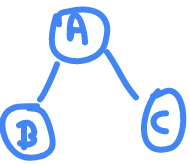
image-20200901191830097

INORDER - L ROOT R - B A C

PREORDER - ROOT L R - A B C

POSTORDER - L R ROOT - B C A

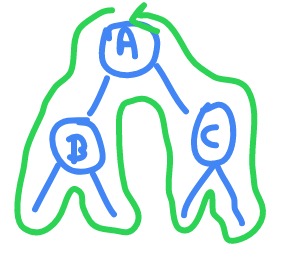
image-20200901192247828

to write each order , we apply this method . First add dummy edges , start from A and first time you see A write it down , same for B and C. And then for inorder if you see A for second time write it and ....

A B C - first time - PRE

B A C - second time - IN

B C A - third time - POST

Implementation and time complexity

all the implementations are recursive manner so go back to recursive section and fully understand how to visualize it.

// INORDER
struct node
{
    int data;
    struct node *left , *right;
}

void Inorder(struct node* t)
{
    if(t != NULL)
    {
        Inorder(t->left); // 1 
        printf("%c" , t->data); // 2 
        Inorder(t->right); // 3
    }
}

to better understand it go back to recursion visualization and try to trace it

time and space complexity are O(n)

to get the other traversal just change the printf location

Double order traversal

this is nothing but print every node twice (not necessarily successive)

example : abbcac

// INORDER
struct node
{
    int data;
    struct node *left , *right;
}

void DO(struct node* t)
{
    if(t != NULL)
    {
        printf("%c" , t->data); // 1
        DO(t->left); // 2
        printf("%c" , t->data); // 3
        DO(t->right); // 4
    }
}

Triple order

void TO(struct node *t)
{
    if(t)
    {
        printf("%c" , t->data); // 1
        TO(t->left); // 2 
        printf("%c" , t->data); // 3
        TO(t->right); // 4
        printf("%c" , t->data); // 5
    }
}

Indirect recursion on tress

void A(struct node *t)
{
    if(t)
    {
        printf("%c" , t->data); // 1
        B(t->left); // 2
        B(t->right); // 3
    }
}

void B(struct node *t)
{
    if(t)
    {
        A(t->left); //1
        printf("%c" , t->data); // 2
        A(t->right); // 3
    }
}

Number of binary trees possible

if we have 1 node , number of binary tress are 1

image-20200901204947660

if we have 2 node , number of binary tress are 2

image-20200901205019982

if we have 3 node , number of binary tress are 5

image-20200901205119486

the pattern here is (2*n)C(n)/(n+1) c is combinator . so we have here (2*3)C3 / 4 = 6C3 / 4 = 20/4 = 5

but if we need to label nodes (put value for every node) is (2*n)C(n) * n! /(n+1)

construct unique Binary tree

We can construct a unique binary tree using combination between 2 of preorder , inorder and postorder

drawing all the combinations of A,B,C,D,E,F..... is time consuming so we are going to prove it with logic.

let's take IN : 1,2,3,4,5,6,7,8 , PRE: 5,3,1,2,4,6,8,7 , POST = ?

to get POST we need to get a unique Binary search tree.

let's take all the cases of IN - L ROOT R and PRE - ROOT L R where L and R are the subtree respectively to left and right.

this is our INORDER

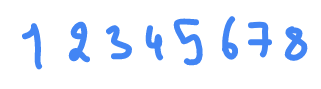
image-20200901213957759

let's say 5 is the ROOT and in the PRE 5 is also the ROOT and all the elements in the right of it will be the L and R

image-20200901214149549

in the left sub tree 1 2 3 4 we look at the PRE we have 3 is the next ROOT

in the right sub tree 6 7 8 the PRE it is 6 8 7 so the ROOT is 6 and 8 7 to the right of it

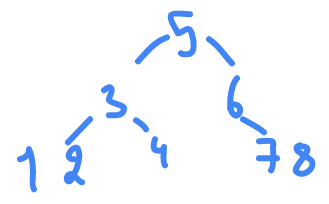
image-20200901214514888

so we have 1 2 in PRE the 2 is to the right of 1 so 2 will fall to the right

for 7 8 in PRE we have 8 is the ROOT and 7 to the left of it

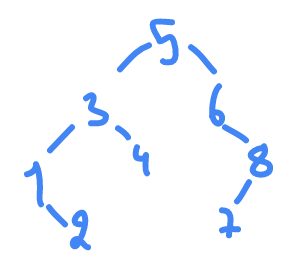
image-20200901214747914

so we form a unique POST binary tree from IN and PRE

if we get the POST of it it's mean print it if it's seen the 3 time.

POST = 2 1 4 3 7 8 6 5

an exercise take POST and IN and form the PRE

Recursive program to count the number of nodes

NN(T) = 1+NN(LST)+NN(RST) and if T is NULL then NN(T)=0

struct node
{
    int i;
    struct node *left , *right;
}

int NN(struct node *t)
{
    if(t)
    {
        int l,r;
        l = NN(t->left); // 1
        r = NN(t->right); // 2
        return (1+l+r); // 3
    }
    else return 0;
}

counting number of leaf

a leaf is a Node with left and right sub trees are NULL

int NL(struct node *t)
{
    if (t == NULL) return 0;
    if(t->left == NULL && t-> right == NULL)
        return 1;
    else
        return (NL(t->left) + NL(t->right));
}

time complexity : O(n)

find the full nodes

full node is the tree who have left and right child

FN(t)   = 0 ; T = NULL
        = 0 ; T is a leaf
        = FN(T->LST) + FN(T->RST); if T has on one child
        = FN(T->LST) + FN(T->RST)+1; if T is full node

int FN(struct node *t)
{
    if(!t) return 0;
    if(!t->left && !t->right) return 0;
    return ( FN(t->left) + FN(t->right)+(t->left && t->right) ) ? 1 : 0;
}

time complexity : O(n)

Recursive program to find the height of a tree

the height is the length of the path to the last leaf you can access

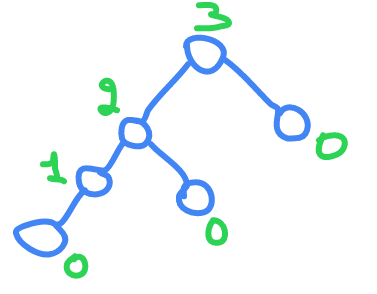
image-20200902122629995

H(t) = {0 ; T is empty
       {0 ; T is a leaf
       {Hmax(H(LST) , H(RST)); otherwise

int H(struct node *t)
{
    if(!t) return 0;
    if( !(t->left) && (!(t->right)) ) return 0;
    int l,r;
    l = H(t->left);
    r = H(t->right);
    return (1+((l>r) ? l : r));
}

Binary search tree

50,15,62,5,20,58,91,3,8,37,60,24

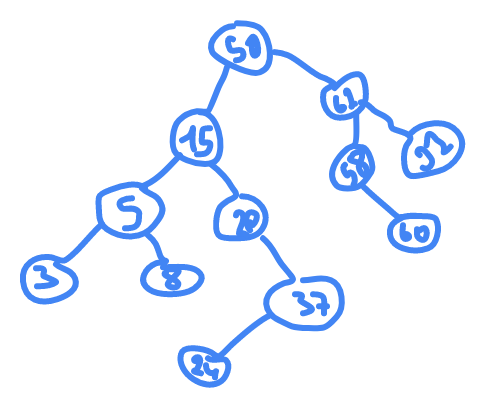
image-20200902123829442

every sub tree in the left is smaller than the root of it and in the right is the higher

INORDER : 3,5,8,15,20,24,37,50,58,60,62,91

so INORDER is nothing but the binary search tree sorted

Binary search tree - POST to IN to PRE

POST ORDER : 10,9,23,22,27,25,15,50,95,60,40,29

we can get directly the INORDER hence is nothing more than the BST sorted

INORDER : 9,10,15,22,23,25,27,29,40,50,60,95

to get that PREORDER we need to draw the tree

the root is 29 since it's the last in the POST , so the root construction is going to be like this , then we go backward 40>29 so it is going to fall to the right and so on..

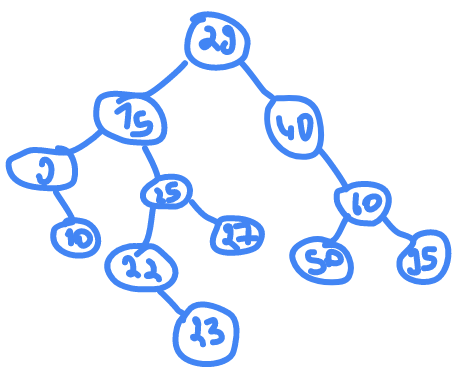
image-20200902125518756

after we trace it we get PREODER : 29,15,9,10,25,22,23,27,40,60,50,95

Number of BST with 3 Distinct keys

1 2 3

image-20200902131102208

2nCn / n+1 = 6C3 / 4 = 20 / 4 = 5

Identify IN-ORDER , PRE-ORDER and POST-ORDER

1 : M B C A F H P Y K

2 : K A M C B Y P F H

3 : M B A C K Y F P H

we have those three trees we don't know what is the type of traversal of each one.

K appear first in 2 and last in 1 so it's the ROOT

after drawing the tree we get
1 is POST , 2 is PRE and 3 is IN

Delete a node from BST

image-20200902180736560

if node is a leaf we can delete it , if node is a Non Leaf and one child the child point to the parent of deleted node. If the node have a subtree we replace the greatest element of it.

Examples:

  • We can delete node 2 without making any changes.

  • We can delete node 25 and point 27 to 30 instead

  • If we need to delete node 15 we replace it with 12

Finding minimum and maximum

find_min(struct node *t)
{
    while(t -> left)    t = t -> left;
}

find_max(struct node *t)
{
    while(t -> right)   t = t -> right;
}

Recursive program on testing type of tree

there is arguing on type of trees those are one of their definition , other reference may differ

complete binary is a tree which have 2 or 0 childrens.
full binary tree mean every layer should be node and last row should be leafs

int iscomplete(struct node *t)
{
    if(t == NULL) return 1;
    if(!t->right && !t->left) return 1;
    else if(t->left && t->right) return (iscomplete(t->left) && iscomplete(t->right));
    else return 0;
}

AVL Trees and balancing

AVL tree (named after inventors Adelson-Velsky and Landis) it's the most popular one there is others like (R-B) and (2-3) the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, re-balancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where nis the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree balancing.

AVL

BF = height(LST)-height(RST) the root should be either {-1,0,1} else we rotated . If it is left-unbalance we rotate it clock wise else opposite clock wise.

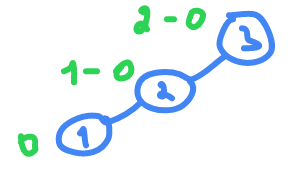
image-20200902184306140

the root is 2 != {-1,0,1} so it's not balanced , and it's left unbalanced so we need to rotate CW

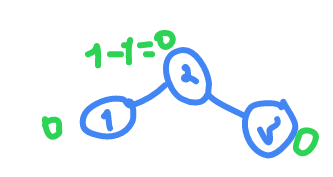
image-20200902184539125

now the root is 0 so now it's balanced.

constructing AVL trees and time complexity

50 , 20 , 60 ,10 , 8 , 15 , 32 ,46 , 11 , 48

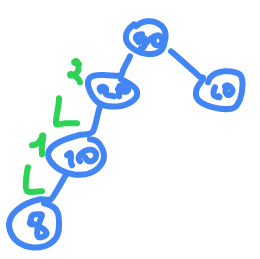
image-20200902185026558

go clock wise

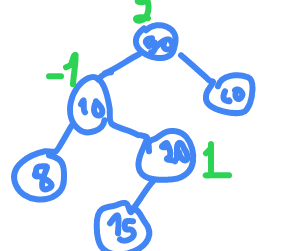
image-20200902185227460

now rotate Anti Clock wise

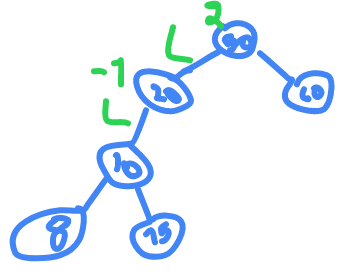
image-20200902185617891

now it's Left-Left so we rotate CW and so on we continue and in the end we get this tree

image-20200902185753117

BSTBalanced BST
searchO(n)O( log n )
heightO(n)O( log n )
InsertionO(n)O(log n)

it's O(log n) because the height is smaller

Minimum and Maximum nodes in AVL tree

S(h) = S(h-1) + S(h-2) + 1

S(1) = 0
S(2) = 1

So let's say h = 6, then S(h = 6) will be (just replacing):

S(6) = S(6-1) + S(6-2) + 1
S(6) = S(5) + S(4) + 1 
S(6) = 2*S(4) + S(3) + 1 + 1
S(6) = 2*(S(3) + S(2) + 1) + S(3) + 2
S(6) = 3*S(3) + 2*S(2) + 4
S(6) = 3*(S(2) + S(1) + 1) + 2*S(2) + 4
S(6) = 5*S(2) + 3*S(1) + 7
S(6) = 5*1 + 3*0 + 7
S(6) = 12

Expression trees

a+b take this and let's draw the tree

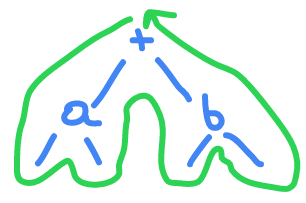
image-20200902201259345

PRE : +ab
IN  : a+b
POST: ab+

a+b*c

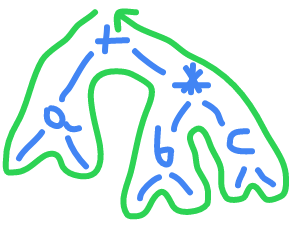
image-20200902201738424

PRE : +a*bc
IN  : a+b*c
POST: abc*+

Various tree representations

The method we see is a pointer to the left and right child , what if we have like 10 childs?

There is a representation called LCRS (Left Child Right Sibling)

image-20200902210603966

image-20200904190326839

LC = 2*i
RC = 2*i+1
Parent = x/2

because it's binary tree multiplying by 2 is nothing but shifting by 1 bit.

if we have i = 2 (base 10) = 10 (base 2) , 2*i = 100 and 2*i+1 = 101 , same for divining by 2 in binary 100/2 = 10

another representation is like this

(Root (a b c) (d e f) ) where (a b c) is LSB of Root and (d e f) is RSB of Root and a is root of LSB and b is left leaf and c is right leaf , same for d e f

This post is also available on DEV.